ஐம்பது கிலோ அழகு உலக அதிசியமோ இல்லையோ தெரியாது, ஆனால் ஆய்லரின் ஆக்கம் நிச்சியம் ஓர் அதிசியம் தான். சரி இதை புரிந்து கொள்ள என்னவெல்லாம் தேவை என்று முதலில் இங்கே பார்ப்போம். பிறகு ஆய்லரின் ஆக்கத்தைக் கொடுக்கிறேன்.
முதலில் பகா எண்கள் என்றால் என்ன என்று பார்ப்போம். எந்த ஓர் இயல் எண் N>1 ணுக்கு ஒன்று மற்றும் அந்த இயல் எண்ணே காரணிகளாக இருந்தால் அந்த எண்ணை ஒரு பகா எண் என அழைக்கிறோம்.
குறிப்பாக,
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,....
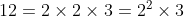
குறிப்பாக எந்த இயல் எண் N > 1 க்கும்,
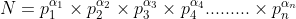
எனலாம்.
எனவே எந்த இயல் எண்ணும் பகா எண்கள் அல்லது பகா எண்களின் அடுக்குக்குறிகளின் (exponents) ஆக்கமாக இருக்கும்.இந்த ஆக்கமும் ஒரு தனித்தன்மை (uniqueness) கொண்டது.
அடுத்தது
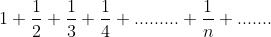
என்ற தொடரின் ஒருங்கல் (convergence) மற்றும் விலகிப் போகும் (divergence) தன்மையைப் பற்றிப் பார்ப்போம்..
இதனை சுருக்கமாக
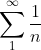
என எழுதலாம்.
1/1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + ...
= ( 1/1 ) + ( 1/2 ) + ( 1/3 + 1/4 ) + ( 1/5 + 1/6 + 1/7 + 1/8 ) + .......
என எழுதலாம்.
மேலும்
( 1/3 + 1/4 ) > (1/4 +1/4)
( 1/5 + 1/6 + 1/7 + 1/8 ) > (1/8+1/8+1/8+1/8)
ஆகும்.
எனவே
1/1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + ... ....
> ( 1/1 ) + ( 1/2 ) + ( 1/4 + 1/4 ) + ( 1/8 + 1/8 + 1/8 + 1/8 ) + ... ...
= 1/1 + 1/2 + 1/2 + 1/2 + 1/2 + ... .....
எனவே இந்தத் தொடரில் மேலும் மேலும் எண்களைக் கூட்டும் போது இந்தத் தொடரின் கூட்டுத் தொகை மிகப் பெரிதாகி முடிவிலியை (infinity) நோக்கிச் செல்கிறது. எனவே இந்தத் தொடர் முடிவிலியை நோக்கி விலகிச் செல்லும் (diverging to infinity) ஒரு தொடராகும்.
அடுத்ததாக பெருக்குத் தொடர் (Geometric series) என்றால் என்ன மற்றும் அதன் கூட்டுத் தொகை என்ன என்றும் பார்க்கலாம்.
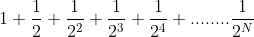
என்ற இந்த தொடர் ஒரு பெருக்குத்தொடராகும்.ஒவ்வொரு அடுத்த எண்ணும் 1/2 ஆல் அதன் முந்தைய எண்ணைப் பெருக்குவதால் கிடைக்கிறது. இப்போது இதன் கூட்டுத் தொகையைப் பார்ப்போம்.
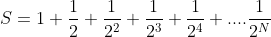
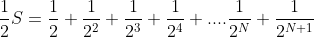
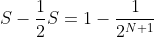
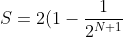)
இப்போது இந்தத் தொடரை முடிவிலி (infinity)வரை செல்ல விட்டால்,
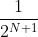
பூஜ்யத்தை நோக்கிச் செல்லும்.
எனவே, S = 2 எனவாகும்.
அதாவது,
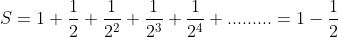
இதே போல்
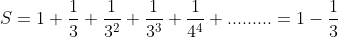
பொதுவாக, எந்த பகா எண் p க்கும்,

என்பது கூட்டுத் தொகையாக இருக்கும்.
இளம் வயதில் படித்த இந்த
(a+b)(c+d) = a(c+d) + b(c+d)
= ac+ad+bc+bd
என்ற இயற்கணிதத்தைப் பயன்படுத்தி
(1+\frac{1}{3}+\frac{1}{3^2{}}+\frac{1}{3^{3}}+.....) = 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{6}+\frac{1}{12}+\frac{1}{18}+.....)
எனக் கண்டறியலாம்.
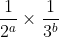
என இருக்கும் எல்லா பின்னங்களின் கூட்டுத் தொகையும், இந்தப்
(1+\frac{1}{3}+\frac{1}{3^{2}}+\frac{1}{3^{3}}+.....))
பெருக்குத் தொகையின் மூலம் கிடைப்பதைப் பார்க்கலாம்.
உதாரணமாக
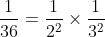
என வருவதைக் காணலாம்.
இறுதியாக,
(1+\frac{1}{3}+\frac{1}{3^{2}}+\frac{1}{3^{3}}+\frac{1}{3^{4}}+.........)(1+\frac{1}{5}+\frac{1}{5^{2}}+\frac{1}{5^{3}}+\frac{1}{5^{4}}+.........)(1+\frac{1}{7}+\frac{1}{7^{2}}+\frac{1}{7^{3}}+\frac{1}{7^{4}}+.........)........ = 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+..........)
எனலாம்.
அதாவது,
(1-\frac{1}{3})(1-\frac{1}{5})(1-\frac{1}{7})......(1-\frac{1}{p})........= \sum_{1}^{\infty }\frac{1}{n})
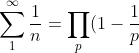) ..........(1)
..........(1)
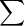
என்பது கூட்டுவதைக் குறித்தால்
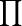
பெருக்குவதைக் குறிக்கிறது.
ஒருவேளை குறிப்பிடும் அளவிலான பகா எண்கள் தான்(finite number of prime numbers) இருக்கிறது எனில், சமன்பாடு (1) இன் வலது பக்கம் கிடைக்கும் எண் அளவிட்டுக் குறிப்பிடும் (finite) எண் N என இருக்கும். ஆனால் சமன்பாடு (1) இன் இடது பக்கத்தில் இருக்கும் தொடரானது முடிவிலியை நோக்கிச் செல்கிறது. அதனால் நிச்சியம் எண்ணிலடங்கா (infinite) பகா எண்கள் இருந்தாக வேண்டும். ஈக்ளுட் (Euclid) கொடுத்த எண்ணிலடங்கா பகா எண்கள் இருக்கும் என்ற நிரூபணம் இங்கே படிக்கலாம்.
இப்போது

என்பதாகும். s = 1 , என இருக்கும் போது கிடைப்பது தான் சமன்பாடு (1 ) . சமன்பாடு (1 ) லிருந்து ஆய்லரின் ஆக்கம் கண்டடைவது மிகச் சுலபம்.
ஆனால் இந்த ஆய்லரின் ஆக்கத்தை விரிவு படுத்தி ரீமான் s ஒரு கலவை எண்ணாக (complex number) இருந்தால் என்ன விளைவு என்ற ஆராய்ந்ததில் பிறந்தது தான் புகழ்பெற்ற இன்றும் தீர்வு கிடைக்காத "Riemann Hypothesis".
என்பதைத் தான் "Riemann-Zeta function" என்றழைக்கிறோம்.
முதலில் பகா எண்கள் என்றால் என்ன என்று பார்ப்போம். எந்த ஓர் இயல் எண் N>1 ணுக்கு ஒன்று மற்றும் அந்த இயல் எண்ணே காரணிகளாக இருந்தால் அந்த எண்ணை ஒரு பகா எண் என அழைக்கிறோம்.
குறிப்பாக,
முதலியவைகள் 100 க்கு கீழே உள்ள பகா எண்களாகும். இந்தப் பகா எண்கள் இயல் எண்களின் கட்டுமான அடுக்குகளாக (building blocks) செயல்படுவதே இதன் சிறப்பாகும். உதாரணமாக 12 என்ற எண்ணை எடுத்துக் கொள்வோம்.
குறிப்பாக எந்த இயல் எண் N > 1 க்கும்,
எனலாம்.
எனவே எந்த இயல் எண்ணும் பகா எண்கள் அல்லது பகா எண்களின் அடுக்குக்குறிகளின் (exponents) ஆக்கமாக இருக்கும்.இந்த ஆக்கமும் ஒரு தனித்தன்மை (uniqueness) கொண்டது.
அடுத்தது
என்ற தொடரின் ஒருங்கல் (convergence) மற்றும் விலகிப் போகும் (divergence) தன்மையைப் பற்றிப் பார்ப்போம்..
இதனை சுருக்கமாக
என எழுதலாம்.
1/1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + ...
= ( 1/1 ) + ( 1/2 ) + ( 1/3 + 1/4 ) + ( 1/5 + 1/6 + 1/7 + 1/8 ) + .......
என எழுதலாம்.
மேலும்
( 1/3 + 1/4 ) > (1/4 +1/4)
( 1/5 + 1/6 + 1/7 + 1/8 ) > (1/8+1/8+1/8+1/8)
ஆகும்.
எனவே
1/1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + ... ....
> ( 1/1 ) + ( 1/2 ) + ( 1/4 + 1/4 ) + ( 1/8 + 1/8 + 1/8 + 1/8 ) + ... ...
= 1/1 + 1/2 + 1/2 + 1/2 + 1/2 + ... .....
எனவே இந்தத் தொடரில் மேலும் மேலும் எண்களைக் கூட்டும் போது இந்தத் தொடரின் கூட்டுத் தொகை மிகப் பெரிதாகி முடிவிலியை (infinity) நோக்கிச் செல்கிறது. எனவே இந்தத் தொடர் முடிவிலியை நோக்கி விலகிச் செல்லும் (diverging to infinity) ஒரு தொடராகும்.
அடுத்ததாக பெருக்குத் தொடர் (Geometric series) என்றால் என்ன மற்றும் அதன் கூட்டுத் தொகை என்ன என்றும் பார்க்கலாம்.
என்ற இந்த தொடர் ஒரு பெருக்குத்தொடராகும்.ஒவ்வொரு அடுத்த எண்ணும் 1/2 ஆல் அதன் முந்தைய எண்ணைப் பெருக்குவதால் கிடைக்கிறது. இப்போது இதன் கூட்டுத் தொகையைப் பார்ப்போம்.
இப்போது இந்தத் தொடரை முடிவிலி (infinity)வரை செல்ல விட்டால்,
பூஜ்யத்தை நோக்கிச் செல்லும்.
எனவே, S = 2 எனவாகும்.
அதாவது,
இதே போல்
பொதுவாக, எந்த பகா எண் p க்கும்,
என்பது கூட்டுத் தொகையாக இருக்கும்.
இளம் வயதில் படித்த இந்த
(a+b)(c+d) = a(c+d) + b(c+d)
= ac+ad+bc+bd
என்ற இயற்கணிதத்தைப் பயன்படுத்தி
எனக் கண்டறியலாம்.
என இருக்கும் எல்லா பின்னங்களின் கூட்டுத் தொகையும், இந்தப்
பெருக்குத் தொகையின் மூலம் கிடைப்பதைப் பார்க்கலாம்.
உதாரணமாக
இறுதியாக,
எனலாம்.
அதாவது,
என்பது கூட்டுவதைக் குறித்தால்
பெருக்குவதைக் குறிக்கிறது.
ஒருவேளை குறிப்பிடும் அளவிலான பகா எண்கள் தான்(finite number of prime numbers) இருக்கிறது எனில், சமன்பாடு (1) இன் வலது பக்கம் கிடைக்கும் எண் அளவிட்டுக் குறிப்பிடும் (finite) எண் N என இருக்கும். ஆனால் சமன்பாடு (1) இன் இடது பக்கத்தில் இருக்கும் தொடரானது முடிவிலியை நோக்கிச் செல்கிறது. அதனால் நிச்சியம் எண்ணிலடங்கா (infinite) பகா எண்கள் இருந்தாக வேண்டும். ஈக்ளுட் (Euclid) கொடுத்த எண்ணிலடங்கா பகா எண்கள் இருக்கும் என்ற நிரூபணம் இங்கே படிக்கலாம்.
இப்போது
ஒரு முழு எண் மற்றும் p ஒரு பகா எண் எனில,்
ஆய்லரின் ஆக்கம்
ஆய்லரின் ஆக்கம்
என்பதாகும். s = 1 , என இருக்கும் போது கிடைப்பது தான் சமன்பாடு (1 ) . சமன்பாடு (1 ) லிருந்து ஆய்லரின் ஆக்கம் கண்டடைவது மிகச் சுலபம்.
ஆனால் இந்த ஆய்லரின் ஆக்கத்தை விரிவு படுத்தி ரீமான் s ஒரு கலவை எண்ணாக (complex number) இருந்தால் என்ன விளைவு என்ற ஆராய்ந்ததில் பிறந்தது தான் புகழ்பெற்ற இன்றும் தீர்வு கிடைக்காத "Riemann Hypothesis".
என்பதைத் தான் "Riemann-Zeta function" என்றழைக்கிறோம்.


